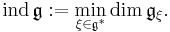Index of a Lie algebra

Lie groups

Classical groups General linear group GL(n) Special linear group SL(n) Orthogonal group O(n) Special orthogonal group SO(n) Unitary group U(n) Special unitary group SU(n) Symplectic group Sp(n)
Simple Lie groups List of simple Lie groups Infinite simple Lie groups: A_n, B_n, C_n, D_n, Exceptional simple Lie groups: G₂ F₄ E₆ E₇ E₈
Other Lie groups Circle group Lorentz group Poincaré group Conformal group Diffeomorphism group Loop group
Lie algebras Exponential map Adjoint representation of a Lie group Adjoint representation of a Lie algebra Killing form Lie point symmetry
Structure of semi-simple Lie groups Dynkin diagrams Cartan subalgebra Root system Real form Complexification Split Lie algebra Compact Lie algebra
Representation theory Representation of a Lie group Representation of a Lie algebra
Lie groups in Physics Particle physics and representation theory Representation theory of the Lorentz group Representation theory of the Poincaré group Representation theory of the Galilean group

Let g be a Lie algebra over a field K. Let further 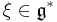$\xi\in\mathfrak{g}^*$ be a one-form on g. The stabilizer g_ξ of ξ is the Lie subalgebra of elements of g that annihilate ξ in the coadjoint representation. The index of the Lie algebra is

$\mathrm{ind}\,\mathfrak{g}:=\min\limits_{\xi\in\mathfrak{g}^*} \mathrm{dim}\,\mathfrak{g}_\xi.$

1 Examples
- 1.1 Reductive Lie algebras
- 1.2 Frobenius Lie algebra
2 References

Examples

Reductive Lie algebras

If g is reductive then ind g = rk g, because the adjoint and coadjoint representation are isomorphic and rk g is the minimal dimension of a stabilizer of an element in g. This is actually the dimension of the stabilizer of any regular element in g.

Frobenius Lie algebra

If ind g=0, then g is called Frobenius Lie algebra. This is equivalent to the fact that the Kirillov form $K_\xi\colon \mathfrak{g\otimes g}\to \mathbb{K}:(X,Y)\mapsto \xi([X,Y])$ is non-singular for some ξ in g^*. Another equivalent condition when g is the Lie algebra of an algebraic group G, is that g is Frobenius if and only if G has an open orbit in g^* under the coadjoint representation.

References

This article incorporates material from index of a Lie algebra on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

Index of a Lie algebra

Contents

Examples

Reductive Lie algebras

Frobenius Lie algebra

References